Introduction 

According to Wikipedia:"Kruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component). Kruskal's algorithm is an example of a greedy algorithm."

In short, Kruskal algorithm is used to connect all nodes in a graph, using the least cost possible.

Example:

A cable TV company is laying cable in a new neighborhood.
An internet Cafe is connecting all PC's via network.

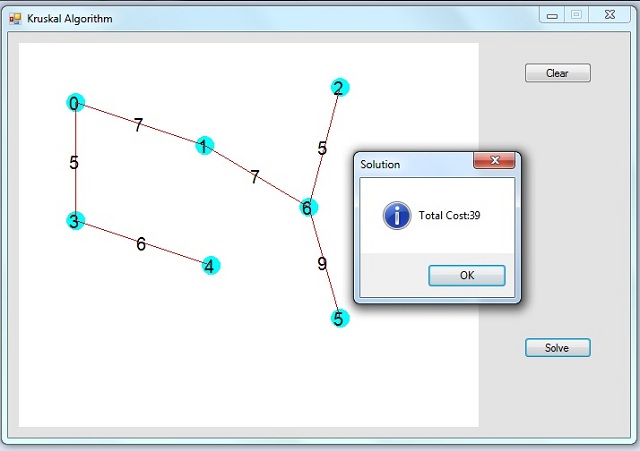
Using the Demo 

Click anywhere to plot the vertices
Hold down ctrl and select two vertices to create edge
A popup window appears to enter edge cost
Having finished plotting the graph, click Solve

Algorithm Break Down

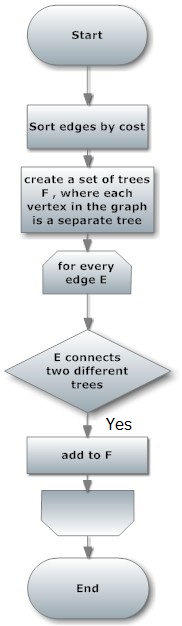
Tricky Part:joining vertices

Besides the vertices and the edges, we have another two lists, m_lstParents and m_lstRanks, we need those to join vertices later.

Parents:Initially every vertex is its own Parent.
Ranks:Initially every vertex has rank zero.

        private void MakeSet()
        {
            m_lstParent = new List<int>(m_lstVertices.Count);
            m_lstRank = new List<int>(m_lstVertices.Count);
            for (int i = 0; i < m_lstVertices.Count; i++)
            {
                m_lstParent.Add(i);
                m_lstRank.Add(0);
            }
        }</int></int>
foreach edge there's 2 vertices, using the recursive function GetParent we'll get their root (parent).

private int GetParent(int nName)
        {
            if (m_lstParent[nName] != nName)// am I my own parent ? (am i the root ?)
            {
                m_lstParent[nName] = GetParent(m_lstParent[nName]);
            }
            return m_lstParent[nName];
        }
if roots are not the same, we have to join the two vertices, depending on their rank 
private void Join(Vertex v1, Vertex v2)
        {
            int v1Parent, v2Parent;
            v1Parent = GetParent(v1.Name);
            v2Parent = GetParent(v2.Name);
            if (m_lstRank[v2Parent] < m_lstRank[v1Parent])//is the rank of  vertex2 parent less than that of vertex1 ?
            {
                m_lstParent[v2Parent] = v1Parent;//yes! then vertex1 is the parent of vertex2 (since he has the higher rank)
            }
            else //rank of vertex2 is greater than or equal to that of vertex1
            {
                m_lstParent[v1Parent] = v2Parent;//make vertex 2 the parent
                if (m_lstRank[v1Parent] == m_lstRank[v2Parent])//both ranks are equal ?
                {
                    m_lstRank[v2Parent]++;//increment one of them, we need to reach a single root for the whole tree
                }
            }
        }

Conclusion

Hope this helped to understand the algorithm clearly, If you have any questions, feel free to ask.

关键字 kruskal,algorithm
推荐.NET配套的通用数据层ORM框架：CYQ.Data 通用数据层框架