Kruskal Algorithm

Introduction
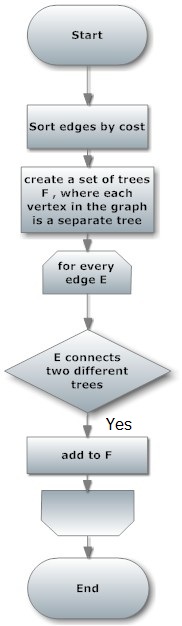
According to Wikipedia:"Kruskal's algorithm is an algorithm in graph theory that finds a minimum spanning tree for a connected weighted graph. This means it finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. If the graph is not connected, then it finds a minimum spanning forest (a minimum spanning tree for each connected component). Kruskal's algorithm is an example of a greedy algorithm."
In short, Kruskal algorithm is used to connect all nodes in a graph, using the least cost possible.
Example:
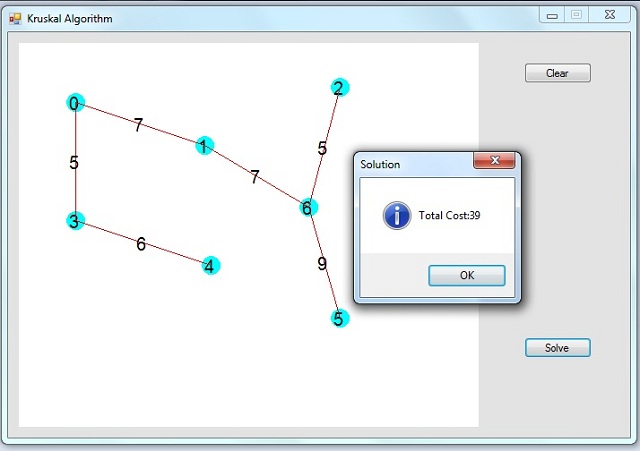
An internet Cafe is connecting all PC's via network.
Using the Demo
Click anywhere to plot the vertices
Hold down ctrl and select two vertices to create edge
A popup window appears to enter edge cost
Having finished plotting the graph, click Solve
Algorithm Break Down
Tricky Part:joining vertices
Besides the vertices and the edges, we have another two lists, m_lstParents and m_lstRanks, we need those to join vertices later.
Parents:Initially every vertex is its own Parent.
Ranks:Initially every vertex has rank zero.
private void MakeSet()
{
m_lstParent = new List<int>(m_lstVertices.Count);
m_lstRank = new List<int>(m_lstVertices.Count);
for (int i = 0; i < m_lstVertices.Count; i++)
{
m_lstParent.Add(i);
m_lstRank.Add(0);
}
}</int></int>
foreach edge there's 2 vertices, using the recursive function GetParent we'll get their root (parent).
private int GetParent(int nName)
{
if (m_lstParent[nName] != nName)// am I my own parent ? (am i the root ?)
{
m_lstParent[nName] = GetParent(m_lstParent[nName]);
}
return m_lstParent[nName];
}
if roots are not the same, we have to join the two vertices, depending on their rank
private void Join(Vertex v1, Vertex v2)
{
int v1Parent, v2Parent;
v1Parent = GetParent(v1.Name);
v2Parent = GetParent(v2.Name);
if (m_lstRank[v2Parent] < m_lstRank[v1Parent])//is the rank of vertex2 parent less than that of vertex1 ?
{
m_lstParent[v2Parent] = v1Parent;//yes! then vertex1 is the parent of vertex2 (since he has the higher rank)
}
else //rank of vertex2 is greater than or equal to that of vertex1
{
m_lstParent[v1Parent] = v2Parent;//make vertex 2 the parent
if (m_lstRank[v1Parent] == m_lstRank[v2Parent])//both ranks are equal ?
{
m_lstRank[v2Parent]++;//increment one of them, we need to reach a single root for the whole tree
}
}
}
Conclusion
Hope this helped to understand the algorithm clearly, If you have any questions, feel free to ask.